Finding the compositions of n

19/6/2016

"A composition of an integer n is a way of writing n as the sum of a sequence of (strictly) positive integers" - Wikipedia.

A composition can include multiple integers of the same value and the order of the values matters, so each unique arrangement of a composition of n is also a distinct composition of n. Each positive integer n has 2^(n-1) compositions. For example 5 has 2^4=16 compositions:

Compositions of 5:
{ 5 }
{ 4, 1 }
{ 1, 4 }
{ 3, 2 }
{ 2, 3 }
{ 3, 1, 1 }
{ 1, 3, 1 }
{ 1, 1, 3 }
{ 2, 2, 1 }
{ 2, 1, 2 }
{ 1, 2, 2 }
{ 2, 1, 1, 1 }
{ 1, 2, 1, 1 }
{ 1, 1, 2, 1 }
{ 1, 1, 1, 2 }
{ 1, 1, 1, 1, 1 }

So why do we care and how do we find them? Well for my purposes I needed to find the compositions of n as part of my honours project, but it seems like something that could come up in all sorts of areas and it was an interesting problem to have to solve. As for how to find them, the point of this post is to share the recursive algorithm I came up with because I think it's rather elegant. This is essentially a more detailed, less formal explanation of my algorithm than what I wrote for Appendix C of my dissertation.

Finding the compositions with only 2 elements

In my project I needed to separately find all the compositions with exactly 2 elements and all the compositions with 3 or more. My algorithm for finding those with 3+ elements can in fact be used to find all compositions, but I thought I might as well share how you would find only those compositions with exactly 2 elements as well.

It's pretty simple really. To find every pair of positive integers which sum to n, just start with n-1 and 1 and keep decrementing the former and incrementing the latter until you have 1 and n-1. Obviously there will be n-1 compositions of n with exactly 2 elements. As an example here's some Lua code:

-- find compositions of n with 2 elements
function comps_2(n)
  local comps = {}
  local left = n-1
  local right = 1
  while left > 0 do
    comps[#comps+1] = {left, right}
    left -= 1
    right += 1
  end
  return comps
end

What follows is a print function, calling code and the resultant output:

function print_comps(comps)
  for c in all(comps) do
    local s = ""
    for e in all(c) do
      s = s..e..", "
    end
    print("{ "..s.."}")
  end
end

n = 5
c2 = comps_2(n)
print(#c2.." compositions of "..n..":")
print_comps(c2)

4 compositions of 5:
{ 4, 1, }
{ 3, 2, }
{ 2, 3, }
{ 1, 4, }

Finding all the compositions of n

The way my algorithm works is conceptually quite simple. You start with the set of n 1s and store a copy, since it's a valid composition of n. Then you remove the last 1 and add it in turn to each of the other numbers, storing the result. This process repeats recursively, backtracking up the recursion whenever the last number isn't a 1.

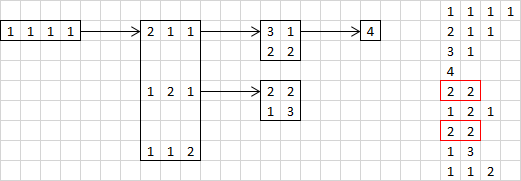
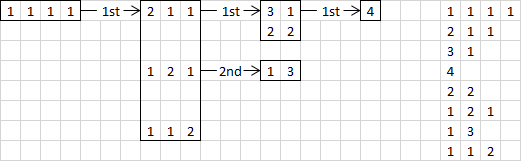
The diagram below illustrates this idea for finding the compositions of 4. The boxes collect all the results garnered from one function call and the arrows show the recursion. First we start with our set of 4 1s. Whenever we encounter an arrow it means 'remove the last 1 and add it to each of the remaining numbers'. The list of compositions found is on the right in the order that they were found (top to bottom). Notice that one of the solutions was found multiple times.

One duplicate set might not seem like much, but we'll be storing exponentially more duplicates as n increases. For example we would store 23 compositions of 5 even though there are only 16 unique compositions. To fix this we just need to start adding the 1 from further into the set. If we find the ith composition within a single function call (box in the diagram) then when we remove the last 1 we start adding it from the ith number in the set. For example:

First we have our set of 1s. We remove the last 1 (giving us { 1, 1, 1 }) and begin to add it to each remaining number in turn, starting with the 1st number. This gives us the set { 2, 1, 1 }, which ends in a 1 so we recurse. This was the 1st composition found in this function call so we start on the 1st number again, getting { 3, 1 }. Again we recurse and get { 4 }, which doesn't end in a 1 so we backtrack. Now we add our 1 to the 2nd number from the { 2, 1, 1 } set, giving us { 2, 2 }. This doesn't end in a 1 so we backtrack. We add a 1 to the 2nd number from our initial set, giving { 1, 2, 1 }. This ends in a 1 so we recurse, but it's the 2nd solution we found in this function call (box) so we start adding from the 2nd number, giving { 1, 3 } instead of duplicating the { 2, 2 } set. Here we backtrack again to get our final composition { 1, 1, 2 }. We know we're done when we've backtracked all the way to our original set.

Below is some Lua code for the complete algorithm, with some calling code at the end and the resulting output afterwards.

-- adds a copy of the source table to the destination table
function add_table_copy(dest, source)
  dest[#dest+1] = {}
  for i = 1, #source do
    dest[#dest][i] = source[i]
  end
end

-- find all compositions of n
function comps_all(n)
  local all_comps = {}
  local comp = {}
  for i = 1, n do
    comp[i] = 1
  end
  add_table_copy(all_comps, comp)
  find_comps(all_comps, comp, 1)
  return all_comps
end

-- recursive composition-finding algorithm
function find_comps(all_comps, comp, start_index)
  --if (#comp <= 3) return
  if (comp[#comp] ~= 1) return
  
  -- remove last element (it's a 1)
  local new_comp = {}
  for i = 1, #comp-1 do
    new_comp[i] = comp[i]
  end
  
  -- add the removed 1 to each element in turn
  local i = start_index
  while i <= #new_comp do
    new_comp[i] += 1
    add_table_copy(all_comps, new_comp)
    find_comps(all_comps, new_comp, i)  -- recurse
    new_comp[i] -= 1
    i += 1
  end
end

n = 5
c = comps_all(n)
print(#c.." compositions of "..n..":")
print_comps(c)

16 compositions of 5:
{ 1, 1, 1, 1, 1, }
{ 2, 1, 1, 1, }
{ 3, 1, 1, }
{ 4, 1, }
{ 5, }
{ 3, 2, }
{ 2, 2, 1, }
{ 2, 3, }
{ 2, 1, 2, }
{ 1, 2, 1, 1, }
{ 1, 3, 1, }
{ 1, 4, }
{ 1, 2, 2, }
{ 1, 1, 2, 1, }
{ 1, 1, 3, }
{ 1, 1, 1, 2, }

I mentioned before that I wanted to be able to find only compositions with 3 or more elements. If you uncomment the first line from the find_comps function then it will do just that. In fact you can set this number to whatever you like and it will only find compositions with at least that many elements. For example:

function find_comps(all_comps, comp, start_index)
  if (#comp <= 3) return
  ...
end

11 compositions of 5:
{ 1, 1, 1, 1, 1, }
{ 2, 1, 1, 1, }
{ 3, 1, 1, }
{ 2, 2, 1, }
{ 2, 1, 2, }
{ 1, 2, 1, 1, }
{ 1, 3, 1, }
{ 1, 2, 2, }
{ 1, 1, 2, 1, }
{ 1, 1, 3, }
{ 1, 1, 1, 2, }

0 Comments