With a long list of things I wanted to demonstrate I decided to design the museum in a modular fashion. Each room would house an exhibit or collection of exhibits demonstrating related techniques. Then I could just plug the rooms next to each other and hey-presto it's the most surreal museum you've ever visited.
The Entrance Hall - Text, HUD text and models
As a side note, the T-Rex model included texture coordinates but no texture. I had a dirt texture for some procedural terrain (more on that later) so I stuck that on the model and it looked suitably fossilised.
Note that the HUD text stays in the same position on the screen regardless of the orientation and position of the camera. This was done by transforming the text to match the position and rotation of the camera, then scaling the text right down and translating it by a small amount along the camera's local z axis to get the text past the near clipping plane and into the viewing frustum. This also means that the HUD text is guaranteed to be closest on the z axis and therefore rendered in front of everything else. Translating in the local x and y positions the text on the screen.
The Garden - Boxing up the sky and connecting modular rooms
Although it has no ceiling, the garden is actually just another instance of the Room class, the same as any other. Each instance of the Room class has a width, height and depth; a position (the x and z parts are the centre of the room, the y is the height of the floor); a bit-field for whether the room has a ceiling, a floor and north, east, south or west walls; and another bit-field for whether the north, east, south or west walls have doors in them. The doors are always the same size and are always positioned in the middle of the wall. So to connect the garden and the entrance hall for example, I simply had to say that the entrance hall had a north wall with a door and the garden had a south wall with a door, then make sure they had the same x and y coordinates (even though the entrance hall is taller) and position them on the z axis such that they just meet (which is easy since we can get their dimensions).
The Procedural Room - Generating geometry,
Sierpinski tetrahedrons and infinite terrain
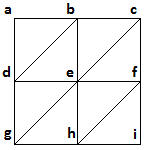
After speaking to my lecturer about it he recommended I try implementing shared normals. Looking at the set of vertices on the right, the normal for vertex e would be the average of the normals for all of the surrounding triangles which feature that vertex. Obviously the shared normal for vertex e will give the best result as it takes into account the most surrounding triangles.
Imagine edge g-h-i as being the bottom, leading edge of the terrain (where new y coordinates are created). I calculate and store the shared normals for vertices e and h because those take into account as many surrounding triangles as possible. By starting with edge a-d-g on the leftmost edge of the terrain and repeating this process until edge c-f-i is on the rightmost edge of the terrain, I calculate shared normals for every vertex along the leading edge and along the row of vertices above it (when on the leftmost or rightmost edges of the terrain, the normals for d and g or f and i respectively are stored). The normals along g-h-i are stored because there is no row below it and therefore no more triangles to take into account. Once the terrain updates, what was g-h-i before is now d-e-f and a new set of heights (and therefore a more complete average) is possible, hence the normals for d-e-f are stored. The normals for a-b-c are never stored because they are simply the previous update's d-e-f, so have already taken into account as many triangles as possible.
At this point the terrain was scrolling infinitely and lighting properly. But due to the way the terrain was generated (just randomised heights) it was very erratic and looked less and less natural as the number of vertices was increased. I thought through how I was going to fix this problem, but didn't have time to implement it. My plan was to have a maximum and minimum height a vertex's y coordinate could be. To calculate a new y coordinate you add a random amount onto the previous y coordinate. The random amount is based on a weighted range covering both positive and negative values. The closer the previous height was to the maximum height, the more the range would be weighted in the negative (and vice versa), thereby forcing the height to remain within the limits. Since each height was based on the previous height, the difference wouldn't be too great and the terrain overall would be smoother. As the number of vertices of the scroll speed increased, the possible random range would decrease as each vertex is now effectively closer to each other vertex. This doesn't take into account the differences in height between adjacent vertices in a row, only between rows, but it was just the start of thinking through the problem.
Read Part 2.










 RSS Feed
RSS Feed
