Download the full procedural methods project here. Read about the turtle graphics and L-systems here. I'll talk about the post-processing in a later post.
Faulting
An interesting side-effect of this process is that you must have a high-resolution mesh to begin with. Each flat face will be represented using many triangles. This may be desirable for lighting or collision purposes with the final terrain, but I wanted to try generating a mesh with the bare minimum number of triangles needed to represent the overall shape. So what if we instead start with a mesh containing just two triangles, then create new vertices and triangles as required with each successive fault?
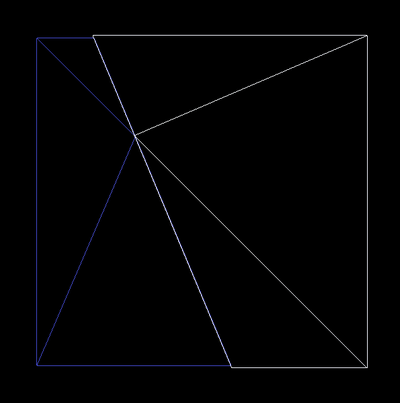
Faulting by adding triangles to a mesh
1. Pick a random perimeter edge from the initial quad.
2. Pick a different random perimeter edge from the initial quad.
3. Pick a random point along each edge.
4. Form the equation of the vertical plane passing through these two
points. This is the cutting plane.
5. For each existing triangle in the set:
a. For each edge of the triangle:
i. Find the intersection point with the cutting plane.
Ignore this if the entire line lies in the plane.
b. Remove duplicate intersections.
c. If there are no intersections, move on to the next triangle.
d. If there is exactly one unique intersection then one vertex of
the triangle lies in the plane and the others are on the same
side. Move on to the next triangle.
e. If there are two intersections:
i. Form a Delaunay triangulation of the set of 5 points
(triangle vertices A, B and C and the two unique
intersection points I0 and I1 along different edges).
ii. Remove the original triangle from the set.
6. Add all triangles formed by Delaunay triangulation to the set.
7. Displace all triangles on one side of the cutting plane.
a. Create vertical quads to fill the holes introduced in the
displacement.
8. Split existing vertical quads along the cutting plane.
9. Displace all vertical quads on one side of the cutting plane.
10. Add the new vertical quads to the set of quads.
 22Can's Godus (2013)
22Can's Godus (2013)
For a low number of faults the additive algorithm produces a terrain with far fewer vertices than the traditional faulting algorithm. For a high number of faults it produces finer detail than could be achieved with a fixed resolution grid, while representing the terrain with the minimal number of vertices possible, at least ideally. In truth the current version of this algorithm ends up producing more triangles than is necessary due to the fact that each triangle is split individually without taking into account adjacent triangles with common edges. This results in more and more, smaller and smaller triangles being added to a section as more faults pass through it. Eventually this artifacts itself as holes in the mesh in areas of cross-section for many faults, as the triangles are now small enough that the vertices are considered the same (floating point rounding errors) and so are removed as duplicates. I'll discuss possible solutions to this problem later on.
In the first version of the algorithm the vertical quads were added to the set of triangles which are split using the Delaunay triangulation. This led to the vertical surfaces also having far more triangles than necessary, but this was a much easier problem to fix. When a horizontal surface is faulted it becomes two arbitrarily-shaped polygons, but when a vertical quad is split it simply becomes two smaller quads. This is why the vertical quads and horizontal triangles are dealt with separately during the faulting process.
The terrain is stored as a collection of triangles and a collection of quads. These triangles and quads are what the faulting algorithm operates on. Only after the faulting process is finished is the vertex buffer for the mesh generated.
Delaunay Triangulation
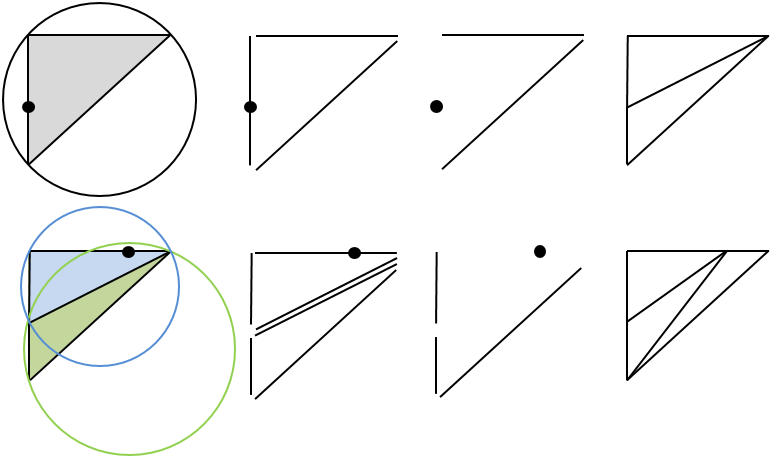
In this application a Delaunay triangulation is always being formed from a set of 5 points, 3 of which form a triangle upon whose edges the other 2 points lie. The algorithm for forming a Delaunay triangulation is as follows:
1. Form the largest possible triangle from the set of 5 points. This is
the Delaunay set. In this case this is already known to be the vertices
A, B and C of the original triangle.
2. Incrementally add the intersection vertices, reforming the triangulation
each time.
To add a vertex:
1. For each existing triangle in the set:
a. If the new vertex lies within that triangle's circumcircle:
i. Store that triangle's edges in the set of edges.
ii. Remove that triangle from the Delaunay set.
2. Remove duplicate edges.
3. Remove edges which are collinear with the new vertex.
4. Form triangles out of each remaining edge in the set and the new vertex.
a. Add these triangles to the Delaunay set.
b. Remove all edges from the edge set.
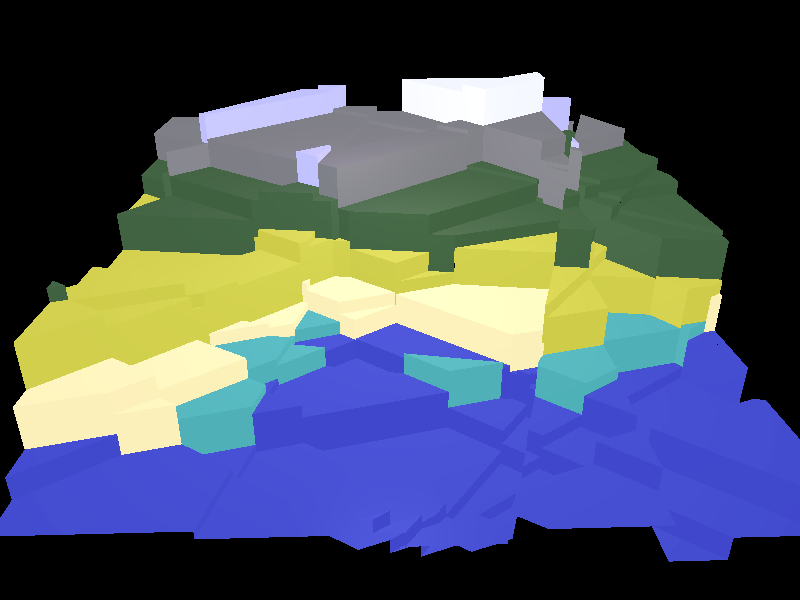
Color banding to produce ‘biomes’
| Snow | Off-white | 5% |
|---|---|---|
| Ice | Light blue | 10% |
| Rock | Grey | 10% |
| Forests | Dark green | 15% |
| Grasslands | Light green | 15% |
| Sand / beaches | Yellow / brown | 10% |
| Shallow water / fresh water | Turquoise | 5% |
| Deep water / salt water | Dark blue | 30% |
Problems and improvements
For horizontal triangles:
1. When an intersection with a triangle is found, find every triangle
with a common edge which also intersects the cutting plane.
a. For each of those triangles, do the same.
2. You now have a horizontal patch of adjacent triangles, all of which
intersect the cutting plane.
3. Take the set of edges of all of the triangles and remove all internal
edges. You now have the outline of a (probably concave) polygon
representing the horizontal patch.
4. Remove all collinear edges.
5. Split any edges which intersect the cutting plane at their intersection
point. Introduce new edges between these intersection points. You now
have a collection of at least 2 adjacent polygons, with a common edge
along the cutting plane.
6. Triangulate each of these polygons independently.
Vertical planes can be dealt with as before. Now that the horizontal
surfaces are minimally complex, the vertical planes needed to fill in the
gaps after extruding the polygons on one side of the cutting plane will
also be minimally complex.
Put simply: each extruded polygon edge requires a vertical plane. By
minimizing the number of edges, we also minimize the number of planes.
This could be fixed using duplication checks when building the vertex and index buffers. Another possible fix would be to change the storage method used by the algorithm and operate on a single set of edges, rather than separate sets of triangles and quads.
Since the cutting plane is formed by connecting two random points on different edges, it is sometimes extremely short, or very closely follows one of the outer edges. These faults don’t tend to add much to the terrain other than additional triangles, so some sort of vetting process for the cutting plane could be implemented to force it to keep picking new points until some desired criteria are met.










 RSS Feed
RSS Feed
