Download the full procedural methods project here.
For an overview of what this is see my previous post.
Gallery
Defining L-systems for turtles
| COMMAND_DRAW COMMAND_MOVE COMMAND_TURN_LEFT COMMAND_TURN_RIGHT COMMAND_PUSH COMMAND_POP COMMAND_NOTHING | Move forward in the direction currently facing while drawing to the texture. Move forward in the direction currently facing, without drawing. Turn left (anticlockwise) by an angle in degrees. Turn right (clockwise) by an angle in degrees. Remember the current orientation and position and push them onto a stack. Revert to the last remembered position and orientation and remove it from the stack. Do nothing (useful for symbols which should not be interpreted by the turtle but which are used to control the evolution of the curve). |
Rules: F → F-F++F-F
Constants: + -
Meanings: F → draw 80%, + → turn right 60°, - → turn left 60°
Axiom: F++F++F
Initial heading: 0
Initial position: x = 0.1, y = 0.75
Scaling factor: 1/3 (exact)
Rules are the set of characters and their productions that comprise the L-system itself. When iterating over the L-system, each character in the current string will be replaced by its production according to these rules (in this example 'F' is replaced with
"F-F++F-F"). Note that every character used in an L-system must define a rule and a meaning. In this example the '+' rule has production "+" and the '-' rule has production "-", i.e. they are constants in the system and are described as such for brevity. Iterating over them in the system simply replaces them with themselves. Note that the → and , characters are never part of the L-system definitions, they are simply part of the layout of this information.
The meaning of a character is the command the turtle should perform when it encounters that character in its command string. Move and draw commands are given in terms of the percentage of the canvas to cover so that they are independent of canvas size. The turn left and right commands are given in degrees for ease of understanding.
The axiom is the starting point of the command string (the 0th iteration of the L-system). The initial heading describes what direction the turtle should be facing at the start of the first drawing (in degrees), where 0 is right and 90 is down. The initial position is the point on the canvas the turtle should begin the first drawing, given as percentages across (0 is the left edge, 1 the right) and up (0 is bottom edge, 1 is top) the canvas.
Finally the scaling factor describes how to scale the move and draw commands in order to fit the drawing on the same size canvas, as each iteration would otherwise result in ever-larger images. The scale s at the nth iteration is based on the scaling factor f such that s = f^n . An example of how this works is given in my previous post in the section "A problem of scale". The scaling factor also includes some combination of the following notes:
- exact: The L-system will cover the exact same amount of canvas at any iteration.
- diminishing expansion: The L-system expands with each iteration to fill a certain area, then covers exactly that area with each further iteration.
- rotates: The L-system rotates with each iteration, usually about the initial position.
- rough: The scaling factor is incorrect and the L-system will eventually shrink to nothing or expand over the boundaries of the canvas.
01 - Koch Snowflake
02 - Koch Antisnowflake
03 - Quadratic Koch A
04 - Quadratic Koch B
05 - Vicsek Fractal (Outline)
06 - Sierpiński Arrowhead
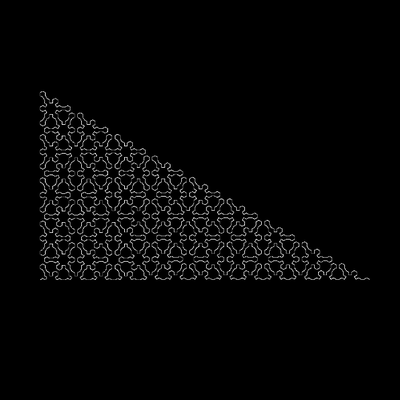
07 - Sierpiński Triangle
08 - Sierpiński Curve
09 - Sierpiński Carpet
10 - Dragon Curve
11 - Terdragon
12 - Lévy C Curve
13 - Hilbert Curve
14 - Hilbert II Curve
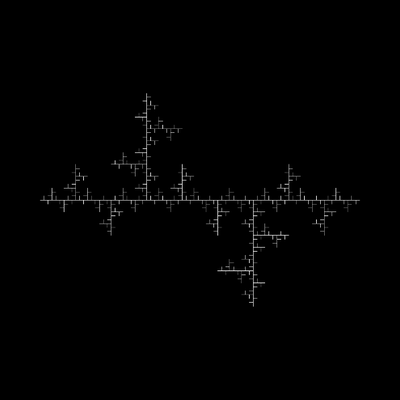
| Rules: X → XFYFX+F+YFXFY-F-XFYFX, Y → YFXFY-F-XFYFX+F+YFXFY Constants: F + - Meanings: X → do nothing, Y → do nothing, F → draw 80%, + → turn left 90°, - → turn right 90° Axiom: X Initial heading: 90 Initial position: x = 0.1, y = 0.9 Scaling factor: 1/3 (diminishing expansion) Note that the 0th iteration is blank. |
15 - Square Space-Filling Tree
16 - Triangle Space-Filling Tree
| Rules: F → G[M|X][|M|X]G[+X+F][F][-X-F], G → GG, M → MM, X → [F] Constants: + - | [ ] Meanings: F → draw 25%, G → draw 25%, M → move 25%, X → do nothing, + → turn left 60°, - → turn right 60°, | → turn 180°, [ → push, ] → pop Axiom: [F]-X-[F]-X-[F]-X Initial heading: 270 Initial position: x = 0.5, y = 0.4 Scaling factor: 0.5 (exact) |
17 - Gosper Curve
18 - Quadratic Gosper
| Rules: X → XFX-YF-YF+FX+FX-YF-YFFX+YF+FXFXYF-FX+YF+FXFX+YF-FXYF-YF-FX+FX+YFYF-, Y → +FXFX-YF-YF+FX+FXYF+FX-YFYF-FX-YF+FXYFYF-FX-YFFX+FX+YF-YF-FX+FX+YFY Constants: F + - Meanings: X → do nothing, Y → do nothing, F → draw 80%, + → turn left 90°, - → turn right 90° Axiom: -YF Initial heading: 0 Initial position: x = 0.1, y = 0.9 Scaling factor: 1/5 (exact) |
19 - Pentagonal
| Rules: F → F++F++F|F-F++F Constants: + - | Meanings: F → draw 50%, + → turn left 36°, - → turn right 36°, | → turn 180° Axiom: F++F++F++F++F Initial heading: 0 Initial position: x = 0.25, y = 0.1 Scaling factor: 2/(3 + √5) (exact) I chose to have a special command for turning 180° rather than using +++++ or ----- to reduce the size of the string this system generates. |
20 - Penrose Tiling
| Rules: M → OA++PA----NA[-OA----MA]++, N → +OA--PA[---MA--NA]+, O → -MA++NA[+++OA++PA]-, P → --OA++++MA[+PA++++NA]--NA, A → nothing Constants: + - [ ] Meanings: M → do nothing, N → do nothing, O → do nothing, P → do nothing, A → draw 50%, + → turn left 36°, - → turn right 36°, [ → push, ] → pop Axiom: [N]++[N]++[N]++[N]++[N] Initial heading: 0 Initial position: x = 0.5, y = 0.5 Scaling factor: 0.6 (exact) Note that the 0th iteration is blank. |
21 - Lace
| Rules: W → +++X--F--ZFX+, X → ---W++F++YFW-, Y → +ZFX--F--Z+++, Z → -YFW++F++Y--- Constants: F + - Meanings: W → do nothing, X → do nothing, Y → do nothing, Z → do nothing, F → draw 50%, + → turn left 30°, - → turn right 30° Axiom: W Initial heading: 0 Initial position: x = 0.1, y = 0.3 Scaling factor: 0.55 (pretty much exact) Note that the 0th iteration is blank. |
22 - Crystal
23 - Islands and Lakes
24 - Cube Effects
| Rules: F → BB[++F][F][--F], B → B[++D][--D]B, D → F, X → F Constants: + - [ ] Meanings: F → draw 50%, B → draw 25%, D → draw 25%, X → do nothing, + → turn left 60°, - → turn right 60°, [ → push, ] → pop Axiom: [F]-X-[F]-X-[F]-X Initial heading: 270 Initial position: x = 0.5, y = 0.4 Scaling factor: 0.5 (exact) |









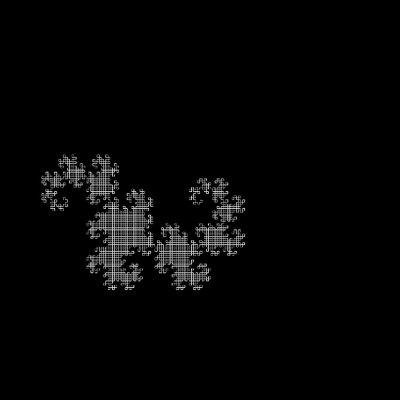
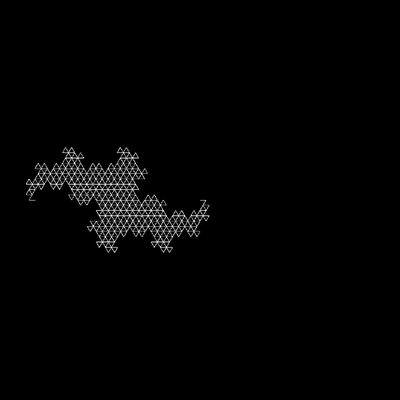












































 RSS Feed
RSS Feed
